基于 Megatron-LM 的 GPU 集群上高效大规模语言模型训练
发布于 • 作者: Deepak Narayanan et al.
介绍
本文是 Efficient Large-Scale Language Model Training on GPU ClustersUsing Megatron-LM的简要阅读翻译
摘要
大型语言模型在多个任务上取得了最先进的准确率。然而，高效训练这些模型极具挑战性，原因主要有两点： (a) GPU 内存容量有限，即使在多 GPU 服务器上也无法容纳超大模型； (b) 所需的计算量巨大，可能导致不切实际的超长训练时间。
因此，提出了新的模型并行方法，例如张量并行和流水线并行。然而，直接使用这些方法在成千上万 GPU 上会遇到扩展性问题。本文展示了如何将张量并行、流水线并行和数据并行进行组合，从而扩展到数千 GPU。我们提出了一种新的交错流水线调度策略，在内存占用与现有方法相当的情况下，可将吞吐量提升 10% 以上。
我们的方法使得在 3072 个 GPU 上以 502 petaFLOP/s 的速度训练一个 1 万亿参数 的模型成为可能（单 GPU 吞吐量达到理论峰值的 52%）。
引言
基于 Transformer 的语言模型在自然语言处理（NLP）领域推动了近年来的快速进展。这得益于大规模计算资源的普及以及数据集规模的不断扩大。近期研究表明，大型语言模型在零样本或小样本学习中表现出色，在多种 NLP 任务和数据集上取得了很高的准确率。
这些大型语言模型在下游应用中具有广泛前景，例如客户反馈摘要、自动对话生成、语义搜索以及代码自动补全。因此，最先进 NLP 模型的参数规模呈指数级增长。
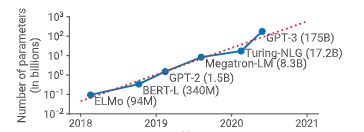图 1：最先进自然语言处理（NLP）模型规模随时间变化的趋势。训练这些模型所需的浮点运算量呈指数级增长。
然而，训练此类模型面临两大挑战： (a) 即使是最大的 GPU，其主存也无法容纳这些模型的全部参数； (b) 即使能够在单个 GPU 上容纳模型，高昂的计算需求也会导致难以接受的训练时间。例如，在单个 V100 GPU 上训练一个拥有 1750 亿参数 的模型，可能需要 约 288 年。
这促使人们采用并行化技术。数据并行通常效果良好，但存在两个限制： (a) 当扩展到一定规模后，单 GPU 的批大小过小，会降低 GPU 利用率并增加通信开销； (b) 可使用的设备数量受限于批大小，从而限制了加速器规模。
为解决这些问题，提出了多种模型并行技术。例如， 张量并行（层内并行） 将 Transformer 层中的矩阵乘法拆分到多个 GPU 上。然而，该方法在模型规模进一步扩大时会遇到瓶颈： (a) 张量并行所需的 all-reduce 通信需要跨服务器进行，速度慢于服务器内的高速互联； (b) 高度的模型并行可能导致矩阵规模过小，从而降低 GPU 利用率。
另一种方法是流水线模型并行，即将模型的不同层分布在多个 GPU 上，并将一个批次划分为多个微批次（microbatches），在这些微批次之间进行流水线执行。为了保持严格的优化器语义，每个批次结束时需要进行流水线刷新，这会造成设备空闲，即流水线气泡，在某些情况下可占用多达 50% 的时间。
在本文中，我们提出了一种新的流水线调度方式，即使在较小批大小下也能提高效率。
用户可以使用多种并行技术来训练大型模型，每种方法都有不同的权衡。这些技术也可以组合使用，但组合后会产生非平凡的相互作用，需要仔细分析才能获得良好性能。
本文试图回答以下问题：
在给定批大小的情况下，如何组合并行技术，以在保持严格优化器语义的同时最大化大型模型的训练吞吐量？
我们展示了如何结合流水线并行、张量并行和数据并行，提出一种称为 PTD-P 的方法，用于在数千 GPU 上高效训练大型语言模型。该方法在多 GPU 服务器内使用张量并行，在服务器之间使用流水线并行，并结合数据并行，从而实现对 万亿参数模型 的可扩展训练。
在实验中，我们在 3072 个 A100 GPU 上实现了接近线性的扩展，单 GPU 端到端训练吞吐量达到 163 teraFLOP/s，总吞吐量达到 502 petaFLOP/s，并估计完整训练时间约为 3 个月。
我们认为这是目前该规模模型所达到的最快训练吞吐量。
在大规模下实现如此高的吞吐量，需要在多个方面进行创新和精细化工程设计，包括：
- 高效的内核实现，使计算主要受限于计算而非内存带宽；
- 智能的计算图划分，以减少跨网络链路传输的数据量并降低设备空闲时间；
- 针对领域的通信优化；
- 先进的硬件支持，包括高性能 GPU 以及服务器内外的高速互联。
我们开源了相关软件（https://github.com/nvidia/megatron-lm），希望能够帮助更多研究团队高效训练大规模 NLP 模型。
基于实验和分析，我们总结了以下经验原则：
- 不同形式的并行会产生复杂的相互作用。并行策略会影响通信量、计算效率以及流水线气泡大小。不合理的张量并行与流水线并行组合，可能导致吞吐量降低 2 倍。
- 流水线调度策略至关重要。我们提出的交错调度在内存占用相当的情况下，可比已有方法提升 10% 的吞吐量。
- 超参数（如微批大小）对性能影响显著，合理设置可将吞吐量提升 15%。
- 在万亿参数模型和数千 GPU 的规模下，通信成为关键瓶颈。更慢的互连或更高通信开销的划分方式都会严重影响扩展性。
并行模式
本节介绍用于训练无法放入单个 GPU 内存的大型模型的并行技术。本文将流水线模型并行和张量模型并行与数据并行相结合，形成 PTD-P 方法。
我们需要注意的是，我们并不会自动探索并行化策略的搜索空间（例如 FlexFlow、PipeDream 以及 DAPPLE等方法），而是提出了一些启发式方法（见第 3 节），这些方法在实践中被证明效果良好。
数据并行
在数据并行中，每个工作节点都保存完整模型的一份拷贝，输入数据集被划分，各节点定期聚合梯度以保持权重一致。对于无法放入单个工作节点的大模型，可以在较小的模型分片上使用数据并行。
流水线模型并行
在流水线并行中，模型的不同层被分布到多个设备上。一个批次被划分为多个微批次，并在这些微批次之间进行流水线执行。
为了保持严格的同步权重更新语义，需要在每个批次开始和结束时进行流水线刷新，这会导致设备空闲，即流水线气泡。我们的目标是尽量减小这种气泡。
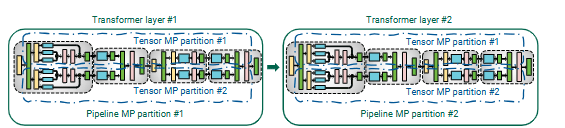图 2：本文在 Transformer 模型中使用的张量并行与流水线并行的组合示意图。
GPipe 提出了一种调度方式：先执行一个批次中所有微批次的前向传播，然后再执行所有微批次的反向传播。
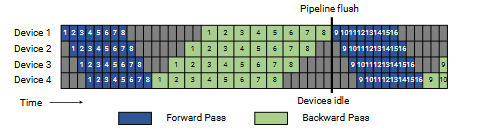图 3：GPipe 流水线调度示意图。蓝色表示前向传播，绿色表示反向传播，灰色区域表示流水线气泡。
在该调度中，流水线气泡由批次开始时的 p−1 次前向传播以及结束时的 p−1 次反向传播组成。设微批数量为 m，流水线阶段数为 p，单个微批前向和反向时间分别为 t_f 和 t_b，则流水线气泡时间为：
$$ t_{pb} = (p - 1) \cdot (t_f + t_b) $$
理想的批次处理时间为：
$$ t_{id} = m \cdot (t_f + t_b) $$
因此，流水线气泡占比为：
$$ \text{气泡时间比例} = \frac{t_{pb}}{t_{id}} = \frac{p - 1}{m} $$
为使流水线气泡时间比例较小，我们需要满足 𝑚 ≫ 𝑝。然而，当 𝑚 很大时，这种方法具有较高的内存占用，因为在整个训练迭代期间，需要为所有 𝑚 个微批次保存中间激活（或者在使用激活重计算时，为每个流水线阶段保存每个微批次的输入激活）。
为此，我们采用 PipeDream-Flush 调度。在该调度中，首先进入一个预热阶段，在该阶段中，各个工作节点执行不同数量的前向传播，如下图所示。在这种调度下，在途微批次（即反向传播尚未完成、需要保留激活的微批次数量）被限制为流水线深度，而不是批次中的微批次数量。
在预热阶段之后，每个工作节点进入稳态阶段，在该阶段中，节点执行一次前向传播随后执行一次反向传播（简称 1F1B）。最后，在一个批次结束时，完成所有剩余在途微批次的反向传播。
该新调度中花费在气泡中的时间与之前相同，但 PipeDream-Flush 调度下未完成前向传播的数量最多为流水线阶段数。因此，该调度仅需为 𝑝 个或更少的微批次保存激活（相比之下，GPipe 调度需要为 𝑚 个微批次保存激活）。因此，当 𝑚 ≫ 𝑝 时，PipeDream-Flush 在内存效率上远优于 GPipe。
为了进一步减小流水线气泡大小，每个设备可以为多个层子集（称为一个模型块）执行计算，而不再只负责一组连续的层。
例如，若之前每个设备负责 4 层（设备 1 负责第 1–4 层，设备 2 负责第 5–8 层，依此类推），现在可以让每个设备负责 两个模型块（每个包含 2 层），即设备 1 负责第 1、2、9、10 层，设备 2 负责第 3、4、11、12 层，依此类推。
在该方案中，流水线中的每个设备被分配多个流水线阶段，而每个阶段的计算量更小。
与之前类似，可以使用“全前向、全反向”的版本，但这会带来较高的内存开销（与 𝑚 成正比）。因此，我们提出了一种交错调度，将前述的内存高效 1F1B 调度加以扩展。该新调度如图所示，并要求一个批次中的微批次数量必须是流水线并行度（设备数量）的整数倍。例如，当有 4 个设备时，微批次数量必须是 4 的倍数。
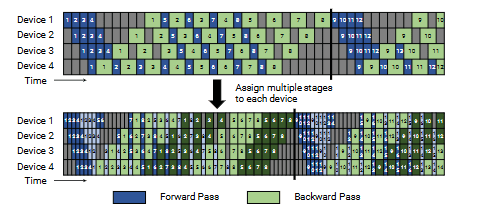图 4：默认 1F1B 流水线调度与交错 1F1B 流水线调度。交错调度中，每个设备被分配多个模型块，流水线刷新更早发生，气泡更小。
如图所示，在新调度中，相同批大小下的流水线刷新会更早发生。若每个设备具有 𝑣 个阶段（或模型块），则每个阶段处理一个微批次的前向和反向时间分别变为 𝑡𝑓 / 𝑣 和 𝑡𝑏 / 𝑣。因此，流水线气泡时间变为：
$$ t^{int}_{pb} = (p - 1) \cdot \frac{t_f + t_b}{v} $$
气泡时间比例为：
$$ \text{气泡时间比例} = \frac{t^{int}{pb}}{t{id}} = \frac{1}{v} \cdot \frac{p - 1}{m} $$
这意味着该新调度将流水线气泡时间减少了 𝑣 倍。然而，这种改进并非没有代价：通信量同样增加了 𝑣 倍。在下一节中，我们将讨论如何利用多 GPU 服务器（例如 DGX A100 节点）中的多张 InfiniBand 网卡来降低额外通信带来的影响。
张量模型并行
在张量模型并行中，模型的单个层被划分到多个设备上。本文采用了 Megatron 在 Transformer 层中使用的划分策略，这是语言模型的核心结构。类似思想也可应用于 CNN 等其他模型。
一个 Transformer 层由自注意力模块和一个 两层的多层感知机（MLP） 组成。
MLP 模块包含两个 GEMM 和一个 GeLU 非线性：
$$ Y = \text{GeLU}(XA), \quad Z = \text{Dropout}(YB) $$
我们沿列方向划分矩阵 $A$：
$$ A = [A_1, A_2] $$
这样可以对每个分块的 GEMM 输出独立应用 GeLU：
$$ [Y_1, Y_2] = [\text{GeLU}(XA_1), \text{GeLU}(XA_2)] $$
这种方式避免了同步需求（若按行划分则需要同步，因为 GeLU 是非线性的）。随后，将第二个权重矩阵 $B$ 按行划分：
$$ B = \begin{bmatrix} B_1 \ B_2 \end{bmatrix}, \quad Y = [Y_1, Y_2] $$
这样可以在两个 GEMM 之间避免通信。第二个 GEMM 的输出随后在 GPU 之间进行归约，再进入 dropout 层。
我们还利用多头注意力中的固有并行性来划分自注意力模块。键（$K$）、查询（$Q$）和值（$V$）矩阵可采用列并行方式划分，输出线性层则直接对注意力模块的分块输出进行操作。
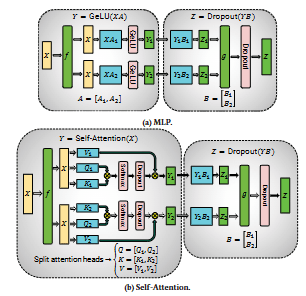图 5：使用张量模型并行划分的 Transformer 模块结构。
该方法在前向传播中仅需 两次 all-reduce，在反向传播中同样需要 两次 all-reduce。其中，算子 f 和 g 是共轭的：f 在前向传播中为恒等映射、在反向传播中执行 all-reduce，而 g 则相反。
并行配置的性能分析
本节分析将流水线并行、张量并行与数据并行相结合后的性能影响。在固定 GPU 数量和批大小的情况下，可以通过不同的 PTD-P 并行度配置来训练模型，而每个维度在内存占用、设备利用率和通信量之间存在权衡。
符号说明
本文使用如下符号：
- $(p, t, d)$：并行维度，分别表示流水线并行度、张量并行度和数据并行度
- $n$：GPU 总数，满足 $p \cdot t \cdot d = n$
- $B$：全局批大小
- $b$：微批大小
- $m = \frac{B}{b \cdot d}$：每个流水线中的微批次数
张量并行与流水线并行
张量并行与流水线并行都可用于将模型参数分布到多个 GPU 上。采用带周期性刷新的流水线并行时，其气泡大小为：
$$ \frac{p - 1}{m} $$
假设 $d = 1$，则 $t \cdot p = n$，气泡大小可写为：
$$ \frac{p - 1}{m} = \frac{n/t - 1}{m} $$
在固定 $B$、$b$ 和 $d$ 的情况下，随着 $t$ 增大，流水线气泡减小。
通信量同样受 $p$ 和 $t$ 的影响。流水线并行使用的是点对点通信，而张量并行需要 all-reduce。对于张量并行，每层在前向和反向传播中各需要两次 all-reduce，总通信量显著增加。当 $t$ 超过单节点 GPU 数量时，跨节点的张量并行通信代价可能过高。
结论一：在 $g$ GPU 服务器上，张量并行通常应使用到 $g$ 的规模；对于更大的模型，应使用流水线并行跨服务器扩展。
数据并行与模型并行
流水线模型并行
令 $t = 1$，则每个流水线的微批次数为：
$$ m = \frac{B}{d \cdot b} $$
流水线阶段数为 $p = n/d$，流水线气泡大小为：
$$ \frac{p - 1}{m} = \frac{n - d}{B/b} $$
随着 $d$ 增大，流水线气泡减小。
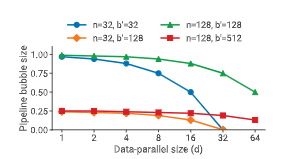图 6：不同 GPU 数量和数据并行规模下，流水线气泡占用时间比例。
数据和张量模型并行
在数据并行中，all-reduce 通信的开销随 $d$ 增大并不会急剧上升，因此总体吞吐量通常会提升。
张量并行需要在每个微批次进行 all-reduce，而数据并行仅需在每个批次进行一次。张量并行还可能导致子矩阵计算规模过小，从而降低 GPU 利用率。
结论二：应首先使用模型并行（$t \cdot p$）使模型参数适配 GPU 内存，再通过数据并行扩展到更多 GPU。
微批大小
微批大小 $b$ 也会显著影响吞吐量。如下图所示，在单 GPU 上，较大的微批大小可将吞吐量提升至 1.3 倍。
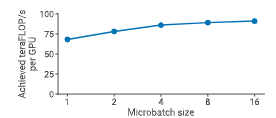图 7：单 GPU 上，不同微批大小下的吞吐量变化。
忽略通信开销时，一个批次的计算时间为：
$$ \left(\frac{B/d}{b} + p - 1\right) \cdot (t_f(b) + t_b(b)) $$
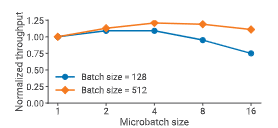图 8：估计吞吐量随微批大小变化的趋势。
结论三：最优微批大小取决于模型特性、流水线深度、数据并行规模以及全局批大小。
激活重计算
激活重计算通过在反向传播前重新执行前向传播来减少内存占用，以增加计算量为代价。该技术对于在流水线并行下训练大型模型至关重要。
若某个阶段包含 $l$ 层，设置 $c$ 个检查点，则内存占用为：
$$ c \cdot A_{input} + \frac{l}{c} \cdot A_{intermediate} $$
当
$$ c = \sqrt{l \cdot \frac{A_{intermediate}}{A_{input}}} $$
时内存占用最小。实践中，通常每 1–2 个 Transformer 层设置一次检查点即可获得最佳效果。
高效的大规模语言模型 GPU 集群训练：Megatron-LM
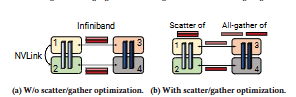图 9：Scatter/Gather 通信优化。(a) 未使用 scatter/gather 优化；(b) 使用 scatter/gather 优化。浅蓝色块表示第一个流水线阶段中的层，深蓝色块表示第二个流水线阶段中的层。若不使用 scatter/gather 优化，同一张量会在跨节点的 InfiniBand 链路上被冗余发送。相反，在发送端可将张量拆分为更小的块，从而减少通过 InfiniBand 发送的张量大小；在接收端再通过 gather 操作将完整张量重新构造。
实现
我们将 PTD-P 实现为 Megatron-LM 代码库的一个扩展，基于 PyTorch 构建，并使用 NCCL 进行设备间通信。为获得高性能，我们针对通信和计算两个方面进行了优化。
通信优化
在使用流水线并行时，我们希望在前向和反向方向上并行发送与接收张量。每台 DGX A100 配备了 8 张 InfiniBand（IB）网卡。然而，流水线中的发送与接收是点对点的，仅发生在两个服务器上的一对 GPU 之间，这使得单次通信难以充分利用全部 8 张 IB 网卡。
我们利用张量模型并行与流水线模型并行同时存在这一事实，来降低跨节点通信的开销。具体而言，在 Transformer 层中，张量模型并行在 MLP 模块的 g 操作之后会使输出在各个张量并行 rank 之间完全复制。因此，相邻流水线阶段中执行张量模型并行的 rank 会发送和接收完全相同的一组张量（如图所示）。
对于足够大的模型，我们采用 张量模型并行度 𝑡 = 8。这意味着，在相邻的多 GPU 服务器之间，相同的一组张量会被重复发送 8 次。为减少这种冗余，我们在发送端将张量拆分为等大小的块，并仅将其中一个块发送给下一节点中对应的 rank，每个 rank 使用其各自的 InfiniBand 网卡进行发送。这样，在 8 路张量并行的情况下，每个块的大小将缩小为原来的 1/8。
在接收端，我们利用 NVLink（其带宽远高于 InfiniBand）执行一次 all-gather，将完整张量重新构造出来。该过程即 scatter/gather 通信优化。
该优化能够更充分地利用 DGX A100 服务器中的多张 IB 网卡，使得通信密集型调度（例如交错流水线调度）在实践中变得可行。
从定量角度看，采用 scatter/gather 优化后，相邻流水线阶段之间需要执行的通信量降为：
$$ \frac{b s h}{t} $$
其中，𝑡 为张量模型并行度，𝑠 为序列长度，ℎ 为隐藏维度。
计算优化
我们对计算图进行了三项模型相关的计算优化，以实现高性能：
-
数据布局优化 在 Transformer 层中更改数据布局，以避免内存密集型的转置操作，并支持带步长的批量 GEMM 内核。具体地，将数据布局从
[b, s, a, h]改为[s, b, a, h]， 其中 𝑏、𝑠、𝑎、ℎ 分别表示批大小、序列长度、注意力头数和隐藏维度。 -
算子融合 使用 PyTorch JIT 为一系列逐元素操作生成融合内核，例如 bias + GeLU 和 bias + dropout + add。
-
自定义 softmax 融合内核 实现两个自定义内核以融合 scale、mask 和 softmax（归约） 操作：
- 一个用于通用掩码（如 BERT）；
- 一个用于隐式因果掩码（如 GPT 等自回归模型）。
这些优化的效果将在下一节中进行量化分析。
实验评估
本节旨在回答以下问题：
- PTD-P 的性能如何？ 是否能实现可行的端到端训练时间？
- 在给定模型和批大小下，流水线并行的扩展性如何？交错调度对性能有多大影响？
- 不同并行维度如何相互作用？诸如微批大小等超参数的影响如何？
- scatter/gather 通信优化的效果如何？在大规模训练时，硬件瓶颈体现在哪些方面？
所有实验均在 Selene 超级计算机 上以混合精度运行。每个节点包含 8 张 NVIDIA 80GB A100 GPU，通过 NVLink 和 NVSwitch 互连。每个节点配备 8 张 200Gbps HDR InfiniBand HCA 用于应用通信，并额外配备 2 张 HCA 用于存储。集群采用三层 fat-tree 拓扑结构，支持高效的 all-reduce 通信。A100 GPU 在 16 位精度下的理论峰值吞吐量为 312 teraFLOP/s。
端到端性能
我们评估了从 10 亿到 1 万亿参数 不同规模 GPT 模型的端到端性能，结合使用张量并行、流水线并行和数据并行（并行度根据第 3 节的经验规则选择）。所有模型均采用 交错流水线调度 并启用 scatter/gather 优化，词表大小为 51,200，序列长度为 2048。
模型参数量 𝑃 可表示为：
$$ P = 12 l h^2 \left(1 + \frac{13}{12h} + V + \frac{s}{12 l h}\right) $$
主要的计算开销来自 Transformer 和 logits 层中的 GEMM，其 FLOPs 数为：
$$ F = 96 B s l h^2 \left(1 + \frac{s}{6h} + \frac{V}{16 l h}\right) $$
| Number of parameters (billion) | Attention heads | Hidden size | Number of layers | Tensor model-parallel size | Pipeline model-parallel size | Number of GPUs | Batch size | Achieved teraFLOP/s per GPU | Percentage of theoretical peak FLOP/s | Achieved aggregate petaFLOP/s |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.7 | 24 | 2304 | 24 | 1 | 1 | 32 | 512 | 137 | 44% | 4.4 |
| 3.6 | 32 | 3072 | 30 | 2 | 1 | 64 | 512 | 138 | 44% | 8.8 |
| 7.5 | 32 | 4096 | 36 | 4 | 1 | 128 | 512 | 142 | 46% | 18.2 |
| 18.4 | 48 | 6144 | 40 | 8 | 1 | 256 | 1024 | 135 | 43% | 34.6 |
| 39.1 | 64 | 8192 | 48 | 8 | 2 | 512 | 1536 | 138 | 44% | 70.8 |
| 76.1 | 80 | 10240 | 60 | 8 | 4 | 1024 | 1792 | 140 | 45% | 143.8 |
| 145.6 | 96 | 12288 | 80 | 8 | 8 | 1536 | 2304 | 148 | 47% | 227.1 |
| 310.1 | 128 | 16384 | 96 | 8 | 16 | 1920 | 2160 | 155 | 50% | 297.4 |
| 529.6 | 128 | 20480 | 105 | 8 | 35 | 2520 | 2520 | 163 | 52% | 410.2 |
| 1008.0 | 160 | 25600 | 128 | 8 | 64 | 3072 | 3072 | 163 | 52% | 502.0 |
表 1：从 10 亿到 1 万亿参数 GPT 模型的弱扩展吞吐量结果。
结果显示，随着模型规模增大，GPU 利用率提升，我们在 3072 张 A100 GPU 上实现了超线性扩展。对于最大模型，达到了 52% 的理论峰值吞吐量。
训练所需的迭代次数为：
$$ I = \frac{T}{B \cdot s} $$
综合推导可得端到端训练时间近似为：
$$ \text{训练时间} \approx \frac{8 T P}{n X} $$
其中 𝑇 为 token 数，𝑛 为 GPU 数量，𝑋 为每 GPU 的实际吞吐量。
例如：
- 1750 亿参数 GPT-3，3000 亿 tokens，在 1024 张 A100 上约需 34 天；
- 1 万亿参数模型，4500 亿 tokens，在 3072 张 A100 上约需 84 天。
与 ZeRO-3 的对比
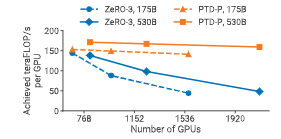图 10：PTD-P 与 ZeRO-3 在不同 GPT 模型上的单 GPU 吞吐量对比。
在相同批大小下，PTD-P 在 175B 和 530B 模型上分别取得 6% 和 24% 的吞吐量提升。随着 GPU 数量增加，PTD-P 的扩展性明显优于 ZeRO-3，在 GPU 数量翻倍时可实现 70% 的性能优势，主要原因是跨节点通信更少。
| Scheme | Number of parameters (billion) | Model-parallel size | Batch size | Number of GPUs | Microbatch size | Achieved teraFLOP/s per GPU | Training time for 300B tokens (days) |
|---|---|---|---|---|---|---|---|
| ZeRO-3 without Model Parallelism | 174.6 | 1 | 1536 | 384 | 4 | 144 | 90 |
| ZeRO-3 without Model Parallelism | 174.6 | 1 | 1536 | 768 | 2 | 88 | 74 |
| ZeRO-3 without Model Parallelism | 174.6 | 1 | 1536 | 1536 | 1 | 44 | 74 |
| ZeRO-3 without Model Parallelism | 529.6 | 1 | 2560* | 640 | 4 | 138 | 169 |
| ZeRO-3 without Model Parallelism | 529.6 | 1 | 2240 | 1120 | 2 | 98 | 137 |
| ZeRO-3 without Model Parallelism | 529.6 | 1 | 2240 | 2240 | 1 | 48 | 140 |
| PTD Parallelism | 174.6 | 96 | 1536 | 384 | 1 | 153 | 84 |
| PTD Parallelism | 174.6 | 96 | 1536 | 768 | 1 | 149 | 43 |
| PTD Parallelism | 174.6 | 96 | 1536 | 1536 | 1 | 141 | 23 |
| PTD Parallelism | 529.6 | 280 | 2240 | 560 | 1 | 171 | 156 |
| PTD Parallelism | 529.6 | 280 | 2240 | 1120 | 1 | 167 | 80 |
| PTD Parallelism | 529.6 | 280 | 2240 | 2240 | 1 | 159 | 42 |
表 2：PTD 并行方式与 ZeRO-3（不使用模型并行）的对比。当在 ZeRO-3 配置下、采用 microbatch size 为 4 时，5300 亿参数的 GPT 模型无法在 560 张 GPU 上完成训练。因此，我们将使用的 GPU 数量增加到 640，并将全局 batch size 提升至 2560，以给出一个吞吐量估计（相关行已在表中用 * 标出）。
流水线并行分析
弱扩展性
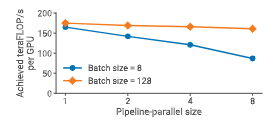图 11：不同批大小下，流水线并行的弱扩展性能。
较大的批大小能够更好地摊销流水线气泡，从而获得更好的扩展性。
交错与非交错调度对比
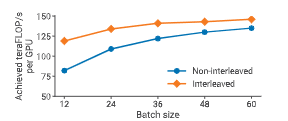图 12：在 1750 亿参数 GPT 模型上，交错与非交错流水线调度的吞吐量对比。
在启用 scatter/gather 优化 后，交错调度在计算性能上优于默认的非交错调度。随着批大小增大，两者差距逐渐缩小：一方面默认调度的气泡减小，另一方面交错调度因通信量更大而优势降低。
并行配置的对比
在本小节中，我们展示了组合不同并行维度所带来的多种权衡。具体而言，我们在相同 GPU 数量下，对给定模型和不同批大小的多种并行配置进行了性能对比。
张量并行与流水线并行
我们评估了在给定模型和批大小下，流水线模型并行与张量模型并行对性能的影响。 图中给出的实验结果表明，为了在训练一个 1610 亿参数 的 GPT 模型（32 个 Transformer 层以支持 32 路流水线并行、128 个注意力头、隐藏维度 20480）时同时获得较低的通信开销和较高的计算资源利用率，张量并行与流水线并行需要结合使用。
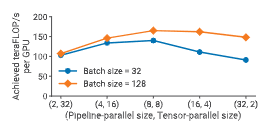图 13：在 64 张 A100 GPU 上，组合流水线并行与张量并行的多种并行配置的单 GPU 吞吐量（GPT 模型，约 1622 亿参数）。
我们观察到，由于 all-reduce 通信代价高昂，张量模型并行最适合在单节点（DGX A100 服务器）内部使用；而流水线模型并行使用的是更廉价的点对点通信，可以跨节点使用而不会成为整个计算的瓶颈。
然而，流水线并行会引入流水线气泡，因此流水线阶段总数应受到限制，使得流水线中的微批次数量是流水线阶段数的合理倍数。综合考虑后，当张量并行度等于单节点 GPU 数量（DGX A100 为 8）时，我们观察到了峰值性能。
这一结果表明，仅使用张量模型并行（如 Megatron）或仅使用流水线模型并行（如 PipeDream 等）都无法达到将两者联合使用时的性能水平。
流水线并行与数据并行
我们在图中评估了一个 59 亿参数 的 GPT 模型（32 个 Transformer 层、32 个注意力头、隐藏维度 3840）中，数据并行与流水线并行对性能的影响。之所以使用较小模型，是因为我们希望展示在模型并行度仅为 2 时仍可容纳模型的情况。为简化分析，这些实验中我们将微批大小固定为 1。
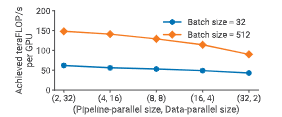图 14：在 64 张 A100 GPU 上，不同批大小下，组合数据并行与流水线并行的单 GPU 吞吐量（GPT 模型，59 亿参数，微批大小为 1）。
可以看到，对于每一种批大小，随着流水线并行度的增加，吞吐量都会下降，这与 §3.3 中的分析模型一致。流水线模型并行应主要用于支持无法放入单个工作节点的大模型训练，而数据并行则更适合用于扩展训练规模。
张量并行与数据并行
我们进一步评估了在同一个 59 亿参数 GPT 模型上，数据并行与张量模型并行的性能影响，如图所示（同样固定微批大小为 1）。
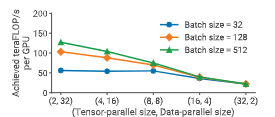图 15：在 64 张 A100 GPU 上，不同批大小下，组合数据并行与张量并行的单 GPU 吞吐量（GPT 模型，59 亿参数，微批大小为 1）。
在较大批大小且微批大小为 1 的情况下，数据并行的通信频率较低；而张量模型并行需要在每一个微批次执行一次 all-to-all 通信。这种通信在端到端训练时间中占据主导地位，尤其是在跨多 GPU 节点执行时。
此外，随着张量并行度的增加，每个 GPU 上执行的矩阵乘法规模变小，从而降低了 GPU 利用率。
需要注意的是，尽管数据并行可以实现高效扩展，但在非常大的模型且训练批大小受限的情况下，仅依赖数据并行是不可行的，原因包括： (a) GPU 内存容量不足； (b) 数据并行本身的扩展性限制。 例如，GPT-3 的收敛训练使用的批大小为 1536，因此仅靠数据并行最多只能扩展到 1536 张 GPU；而为了在合理时间内完成训练，实际使用了约 1 万张 GPU。
微批大小
我们在图中评估了微批大小对组合使用流水线并行与张量并行配置性能的影响。实验使用的是一个 910 亿参数 的 GPT 模型，配置为 $(t, p) = (8, 8)$，并在两种不同批大小下进行测试。
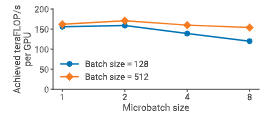图 16：在 64 张 A100 GPU 上，不同微批大小下，$(t, p) = (8, 8)$ 并行配置的单 GPU 吞吐量（GPT 模型，910 亿参数）。
对于该模型，最优微批大小为 2；而对于其他模型，最优微批大小可能不同，具有明显的模型依赖性。
在给定批大小下，增大微批大小会减少流水线中的微批数量 $m$，从而增大流水线气泡；但与此同时，更大的微批大小也可能通过提高内核的算术强度来提升 GPU 利用率。这两个因素相互制衡，使得最优微批大小的选择较为困难。§3.3 中给出的分析模型可以较好地近似真实性能，用作选择该超参数的参考。
激活重计算
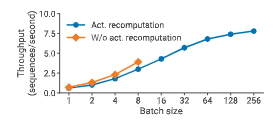图 17：在 128 张 A100 GPU 上，使用与不使用激活重计算时的吞吐量对比（GPT 模型，1450 亿参数，$(t, p) = (8, 16)$）。
图中展示了一个 1450 亿参数 GPT 模型在使用与不使用激活重计算时的吞吐量对比。对于较小批大小，激活重计算由于在反向传播中需要执行一次额外的前向传播，导致吞吐量最多下降 33%（以每秒序列数计）。
然而，激活重计算是支持更大批大小所必需的。在大批大小下，使用激活重计算的吞吐量可达到不使用激活重计算（在较小批大小下）最佳吞吐量的 2 倍，主要原因是流水线气泡更小。
Scatter/Gather 优化
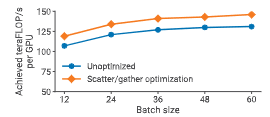图 18：在 96 张 A100 GPU 上，使用与不使用 scatter/gather 通信优化时的单 GPU 吞吐量（GPT-3，1750 亿参数，交错流水线调度）。
对于通信密集型调度（例如大批大小 + 交错流水线），通过减少跨节点通信量，scatter/gather 优化可带来最高约 11% 的吞吐量提升。
融合算子
我们还评估了 §4.2 中所述的算子融合对性能的影响。
- 对于 1750 亿参数 GPT-3 模型，吞吐量提升 19%（从 113 teraFLOP/s 提升至 135 teraFLOP/s，每 GPU）；
- 对于 5300 亿参数 GPT 模型，吞吐量提升 11%（从 133 teraFLOP/s 提升至 148 teraFLOP/s，每 GPU）。
跨节点通信带宽
我们取得的强性能结果，来源于优化的软件与硬件栈的协同使用。在 1 万亿参数模型、3072 张 GPU 的实验中，我们观测到：
- 流水线阶段之间的点对点通信的有效双向带宽为 892 GB/s；
- 数据并行副本之间 all-reduce 操作的有效双向带宽为 12.9 TB/s。
若对算子在设备间的划分不够优化，将导致更多跨节点通信，从而显著削弱扩展性能。
检查点加载与保存
在训练超大模型时，检查点的加载与保存是一个重要的实际问题。例如，1 万亿参数模型的单个检查点大小为 13.8 TB。
在该模型中，所有 384 个节点（3072 张 GPU） 同时加载初始检查点时，峰值读取带宽达到 1 TB/s，已达到并行文件系统的最大读取吞吐量。检查点保存时的写入带宽达到峰值的 40%（273 GB/s）。
相关工作
本节讨论其他用于大规模模型训练的技术。
大模型并行化
流水线模型并行是一种常见的大模型训练技术，其形式多样。本文采用的方式通过流水线刷新来保证严格的优化器语义。
- TeraPipe 在单个训练序列内、跨 token 实现细粒度流水线并行，适用于 GPT 等自回归模型。
- PipeTransformer 通过冻结“稳定”权重的层，动态调整流水线并行与数据并行的比例。
- HetPipe 在异构加速器上结合使用流水线并行与数据并行。
还有一些采用宽松语义的流水线并行方法，例如：
- PipeDream-2BW 通过维护两套权重版本，实现 1 步滞后的权重更新；
- PipeMare 和 Kosson 等工作采用异步流水线并行。
这些方法在吞吐量上优于带刷新机制的流水线方案，但可能会影响收敛速度或最终精度。此外，单独使用流水线并行的扩展性仍受限于模型层数。
PipeDream 将流水线并行与数据并行进行系统化结合，以减少跨设备通信。 DeepSpeed 结合流水线并行、张量并行和数据并行，训练了万亿参数模型，但其吞吐量（约 36% 峰值）低于本文方法（约 52% 峰值），原因包括：
- 更充分的算子融合，使计算保持为计算受限；
- 更高效的流水线调度以减小气泡；
- 更快的硬件（A100 对比 V100，以及更高带宽的互连）；
- 更大规模的 GPU 扩展。
更高的吞吐量使得约 3 个月的训练时间成为可能；若吞吐量仅为 37.6 petaFLOP/s，训练同规模模型将需要 约 40 个月。
Mesh-TensorFlow 提供了一种语言，用于方便地指定组合数据并行与模型并行的策略。 Switch Transformers 利用 Mesh-TensorFlow 训练了一个 1.6 万亿参数 的稀疏激活专家模型，相比 T5-11B 在预训练速度上有显著提升。
分片数据并行
作为 MLPerf 0.6 性能优化的一部分，引入了分片数据并行，即将优化器状态在数据并行工作节点之间进行分片。该方法具有两个优点： (a) 相比于普通数据并行，不会引入额外的通信； (b) 将优化器的计算与内存开销分摊到各个数据并行分区上。
ZeRO 在此基础上进一步扩展：将权重参数和梯度也在数据并行工作节点之间进行分片，并在计算前从其“拥有者”节点拉取所需状态。这会引入额外通信，但可以通过精心设计的计算与通信重叠来部分隐藏。然而，如果未使用张量并行或批大小不足以隐藏额外通信开销，这种方式会变得更困难（如图所示）。
ZeRO-Infinity 利用 NVMe 高效地进行参数交换，使得在少量 GPU 上训练超大模型成为可能。需要指出的是，使用很少的 GPU训练非常大的模型会导致不现实的训练时间（例如需要数千年才能收敛）。
自动划分
FlexFlow、PipeDream、DAPPLE 以及 Tarnawski 等工作，借助代价模型对模型训练图进行自动划分。然而，这些方法并未同时考虑本文讨论的所有并行维度：流水线并行、张量并行、数据并行、微批大小，以及激活重计算等内存节省优化对超出单加速器内存容量的大模型训练的影响。引入这些维度会显著扩大需要探索的搜索空间。 Gholami 等展示了如何对数据并行与模型并行组合的通信成本进行建模。
用于模型训练的 HPC 技术
Goyal 等与 You 等展示了利用高性能计算（HPC）技术在数分钟内训练出高精度的 ImageNet 模型。然而，这些图像分类模型可以轻松放入单个加速器内存，无需模型并行；它们支持非常大的批大小（>32k），从而以较低通信频率将数据并行扩展到大量工作节点；并且模型由紧凑的卷积层组成，天然适合数据并行通信。
讨论与结论
本文展示了如何将 PTD-P（跨节点流水线并行、节点内张量并行、数据并行）进行组合，在训练万亿参数规模模型时实现高聚合吞吐量（502 petaFLOP/s），从而将端到端训练时间控制在合理范围（对万亿参数模型的估计训练时间约为 3 个月）。我们讨论了各类并行方式的权衡关系，以及它们在组合使用时需要谨慎考虑的相互作用。
尽管本文的实现与评估以 GPU 为中心，但其中许多思想同样适用于其他类型的加速器。具体而言，以下思想与加速器无关： (a) 智能划分训练计算图，在保持设备高利用率的同时最小化通信量； (b) 通过算子融合与精心的数据布局，尽量减少内存受限内核； (c) 其他领域特定优化（如 scatter-gather 优化）。
致谢
我们感谢匿名审稿人，以及 Seonmyeong Bak、Keshav Santhanam、Trevor Gale、Dimitrios Vytiniotis 和 Siddharth Karamcheti 的帮助与反馈，这些都改进了本工作。本研究部分得到了 NSF 研究生奖学金（DGE-1656518）和 NSF CAREER 项目（CNS-1651570）的支持。文中观点、发现与结论仅代表作者本人。
附录：浮点运算量
本节说明如何计算模型中的浮点运算次数（FLOPs）。考虑一个语言模型，其包含 𝑙 个 Transformer 层，隐藏维度为 ℎ，序列长度为 𝑠，词表大小为 𝑉，训练批大小为 𝐵。
一个 $A_{m\times k} \times X_{k\times n}$ 的矩阵乘法需要 $$ 2 mkn $$ 次 FLOPs（系数 2 用于计入乘法与加法）。
一个 Transformer 层由注意力模块和一个两层前馈网络组成。对于注意力模块，主要 FLOP 来源包括：
- key、query、value 变换：$6B s h^2$
- 注意力矩阵计算：$2B s^2 h$
- 对 value 的注意力加权：$2B s^2 h$
- 注意力后的线性投影：$2B s h^2$
前馈网络先将隐藏维度扩展到 $4h$，再缩回到 $h$，需要 $$ 16B s h^2 $$ 次 FLOPs。
将上述项相加，每个 Transformer 层在前向传播中产生 $$ 24B s h^2 + 4B s^2 h $$ 次 FLOPs。
反向传播需要两倍 FLOPs，因为需要对输入和权重计算梯度。此外，我们使用了激活重计算，在反向传播前还需执行一次前向传播。因此，每个 Transformer 层的总 FLOPs 为：
$$ 4 \times (24B s h^2 + 4B s^2 h) = 96B s h^2 \left(1 + \frac{s}{6h}\right) $$
另一个主要 FLOP 来源是语言模型头部的 logit 层，其将特征维度 ℎ 映射到词表维度 𝑉。该操作在前向传播中需要 $2B s h V$ FLOPs，在反向传播中需要 $4B s h V$ FLOPs，总计：
$$ 6B s h V $$
因此，对于包含 𝑙 个 Transformer 层的模型，其总 FLOPs 为：
$$ 96B s l h^2 \left(1 + \frac{s}{6h} + \frac{V}{16 l h}\right) $$