ThinkLab

介绍

TrainVerify: Equivalence-Based Verification forDistributed LLM Training的阅读笔记

笔记

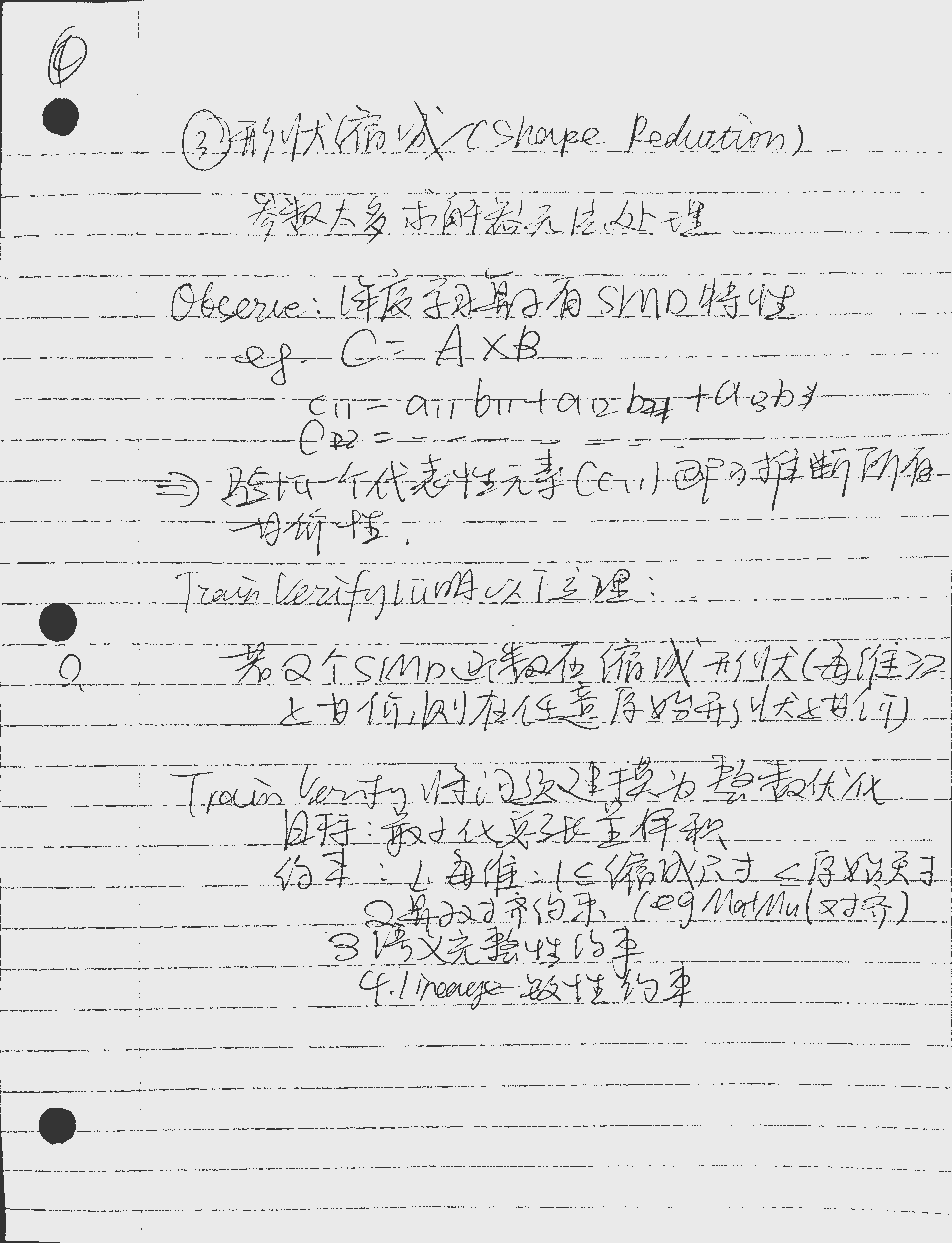
notes notes notes notes notes notes notes

伪代码：形状缩减求解器

def infer_min_shapes(logical_graph, parallel_graph, lineage):
    constraints = []
    
    # 约束1: 每维尺寸 ∈ [1, 原始尺寸]
    for tensor in all_tensors:
        for dim in range(tensor.ndim):
            constraints.add(1 <= tensor.rx_shape[dim] <= tensor.shape[dim])
    
    # 约束2: 算子对齐（如 MatMul 要求 A 的列数 = B 的行数）
    for op in all_operators:
        constraints.add(op.shape_alignment_constraints())
        # 例: MatMul([M,K] × [K,N]) → [M,N] 
        #      ⇒ rx_M_A == rx_M_C, rx_K_A == rx_K_B, rx_N_B == rx_N_C
    
    # 约束3: 语义完整性（保留关键计算模式）
    for op in all_operators:
        constraints.add(op.semantic_intactness_constraints())
        # 例: MatMul 的 K 维（累加维度）必须 ≥2
        #      ReduceSum 的缩减维度必须 ≥2
    
    # 约束4: 血缘一致性（逻辑/并行张量形状匹配）
    for (logical_tensor, parallel_tensor) in lineage_pairs:
        constraints.add(logical_tensor.rx_shape[dim] 
                      == sum(shard.rx_shape[dim] for shard in parallel_tensor.shards))
    
    # 优化目标: 最小化总张量体积（近似求解复杂度）
    objective = minimize(sum(prod(tensor.rx_shape) for tensor in all_tensors))
    
    return solve_integer_optimization(objective, constraints)

详细示例

步骤 1：定义逻辑模型（单设备视角）

首先，开发者编写标准的单设备 PyTorch 代码，作为黄金标准：

# logical_model.py - 逻辑模型定义（单设备）
import torch
import torch.nn as nn

class SimpleLinear(nn.Module):
    def __init__(self, in_features=4, out_features=4):
        super().__init__()
        self.weight = nn.Parameter(torch.randn(out_features, in_features))
    
    def forward(self, x):
        # 前向：y = x @ W^T
        return torch.matmul(x, self.weight.t())

关键点：此代码是设备无关的，代表模型的数学定义，将作为验证的“规范”（specification）。

步骤 2：生成并行化执行计划（2路张量并行）

使用 nnScaler（或其他自动并行框架）将逻辑模型转换为分布式执行计划：

# parallelized_plan.py - 并行化后的执行计划（2路张量并行）
import torch
import torch.distributed as dist

class ParallelLinear:
    def __init__(self, rank, world_size=2):
        self.rank = rank
        self.world_size = world_size
        
        # 按输出维度切分权重：W[0:2, :] 放在 GPU0, W[2:4, :] 放在 GPU1
        self.weight_shard = torch.randn(2, 4)  # 每个GPU持有部分权重
    
    def forward(self, x):
        # 每个GPU计算部分输出：y_i = x @ W_i^T
        partial_y = torch.matmul(x, self.weight_shard.t())
        return partial_y  # 无需通信（前向已正确切分）
    
    def backward(self, grad_output):
        # 计算输入梯度：grad_x_i = grad_output_i @ W_i
        grad_x_partial = torch.matmul(grad_output, self.weight_shard)
        
        # BUG! 正确实现应在此处添加 AllReduce 同步 grad_x
        # 正确代码: dist.all_reduce(grad_x_partial, op=dist.ReduceOp.SUM)
        # 但我们故意遗漏它来演示 bug 检测
        
        # 计算权重梯度（局部，无需同步）
        grad_weight = torch.matmul(grad_output.t(), x)  # shape: [2, 4]
        return grad_x_partial, grad_weight

️Bug 引入：在 backward() 中遗漏了 all_reduce。这会导致每个 GPU 的输入梯度 grad_x 只包含局部贡献，而非全局梯度。这是分布式训练中典型的“静默错误”——训练看似正常，但模型学到了错误参数。

步骤 3：提取数据流图（DFG）

TrainVerify 通过追踪（tracing）提取两个图：

逻辑 DFG（单设备）

输入 x ──► [MatMul: x @ W^T] ──► 输出 y
                ▲
                │
              权重 W

反向:
grad_y ──► [MatMul: grad_y @ W] ──► grad_x (完整梯度)
           [MatMul: grad_y^T @ x] ──► grad_W

并行 DFG（2 GPU）

GPU0:                          GPU1:
x ──► [MatMul: x@W0^T] ──► y0   x ──► [MatMul: x@W1^T] ──► y1

反向 (GPU0):                   反向 (GPU1):
grad_y0 ──► [MatMul] ──► gx0   grad_y1 ──► [MatMul] ──► gx1
            (遗漏AllReduce!)                (遗漏AllReduce!)

关键元数据：张量血缘（Lineage）

逻辑输出 y → 并行输出 [y0, y1]，重组规则：y = concat([y0, y1], dim=-1)

逻辑梯度 grad_x → 并行梯度 [gx0, gx1]，正确重组规则：grad_x = gx0 + gx1（需 AllReduce）

但当前实现中，gx0 和 gx1 未同步，违反血缘约束

步骤 4：构建符号化数据流图（sDFG）

TrainVerify 将具体数值替换为符号变量：

# symbolic_representation.py - 符号化表示
from z3 import Real, simplify

# 逻辑模型符号化
x = [[Real(f'x_{i}{j}') for j in range(4)] for i in range(2)]  # shape [2,4]
W = [[Real(f'w_{i}{j}') for j in range(4)] for i in range(4)]  # shape [4,4]

# 前向：y = x @ W^T
y_logical = [
    [sum(x[i][k] * W[j][k] for k in range(4)) for j in range(4)]
    for i in range(2)
]

# 反向：grad_x = grad_y @ W
grad_y = [[Real(f'gy_{i}{j}') for j in range(4)] for i in range(2)]
grad_x_logical = [
    [sum(grad_y[i][k] * W[k][j] for k in range(4)) for j in range(4)]
    for i in range(2)
]

# 并行模型符号化（2路切分）
W0 = [W[0], W[1]]  # GPU0 权重分片
W1 = [W[2], W[3]]  # GPU1 权重分片

# 前向（正确）：
y0 = [[sum(x[i][k] * W0[j][k] for k in range(4)) for j in range(2)] for i in range(2)]
y1 = [[sum(x[i][k] * W1[j][k] for k in range(4)) for j in range(2)] for i in range(2)]

# 反向（有 bug - 遗漏 AllReduce）：
gx0 = [[sum(grad_y[i][k] * W0[k][j] for k in range(2)) for j in range(4)] for i in range(2)]
gx1 = [[sum(grad_y[i][k+2] * W1[k][j] for k in range(2)) for j in range(4)] for i in range(2)]
# 注意：gx0 只用了 grad_y 的前2列，gx1 只用了后2列 → 未累加！

优势：符号化消除了浮点噪声，聚焦数学语义。gx0 + gx1 应等于 grad_x_logical，但当前实现不满足。

步骤 5：应用形状缩减（Shape Reduction）

原始张量形状 [2, 4] → 缩减为最小可行形状 [2, 2]（每维 ≥2 以保留语义）：

# shape_reduction.py - 形状缩减算法
def infer_min_shapes():
    constraints = []
    
    # 约束1: 每维尺寸 ∈ [1, 原始尺寸]
    constraints.append((1 <= rx <= 2, 1 <= ry <= 4))
    
    # 约束2: 算子对齐（MatMul 要求内维相等）
    constraints.append(rx_inner == ry_inner)  # 例如 K 维必须一致
    
    # 约束3: 语义完整性（累加维度需 ≥2）
    constraints.append(ry_inner >= 2)  # 保证体现累加语义
    
    # 约束4: 血缘一致性（逻辑/并行张量形状匹配）
    constraints.append(ry_logical == ry0 + ry1)  # 输出维度需可拼接
    
    # 求解最小体积
    min_volume = minimize(rx * ry, constraints)
    return min_volume  # 返回: rx=2, ry=2

缩减后验证：

逻辑梯度（单元素示例）：grad_x[0,0] = gy[0,0]*w[0,0] + gy[0,1]*w[1,0] + gy[0,2]*w[2,0] + gy[0,3]*w[3,0]
并行梯度（GPU0）：gx0[0,0] = gy[0,0]*w[0,0] + gy[0,1]*w[1,0] ❌ 缺少后两项
并行梯度（GPU1）：gx1[0,0] = gy[0,2]*w[2,0] + gy[0,3]*w[3,0] ❌ 缺少前两项
验证失败：gx0[0,0] + gx1[0,0] ≠ grad_x[0,0]（因未执行 AllReduce，两者未相加）

数学保证：根据论文 §6 的定理，若缩减形状 [2,2] 上不等价，则原始形状 [2,4] 也必然不等价。

步骤 6：分阶段验证 + SMT 求解

TrainVerify 将图划分为阶段（此处仅1个阶段），并行调用 Z3 求解器：

# staged_verification.py - 验证核心逻辑
from z3 import Solver, sat, unsat

def verify_stage():
    s = Solver()
    
    # 输入等价性（血缘保证）
    s.add(x_gpu0 == x_logical)
    s.add(x_gpu1 == x_logical)
    
    # 目标：输出梯度应满足血缘重组规则
    # 正确应为: grad_x_logical == gx0 + gx1
    # 但当前实现: grad_x_logical != gx0 且 grad_x_logical != gx1
    
    # 添加等价性断言
    s.add(Not(  # 反证：假设等价成立
        ForAll([x, grad_y, W], 
            grad_x_logical[0][0] == gx0[0][0] + gx1[0][0]
        )
    ))
    
    # 求解
    result = s.check()
    
    if result == sat:
        # 找到反例！
        model = s.model()
        print("验证失败！反例：")
        print(f"  x = {model[x[0][0]]}, {model[x[0][1]]}")
        print(f"  grad_y = {model[grad_y[0][0]]}, {model[grad_y[0][1]]}")
        print(f"  grad_x_logical = {model.eval(grad_x_logical[0][0])}")
        print(f"  gx0 + gx1 = {model.eval(gx0[0][0] + gx1[0][0])}")
        return False
    else:
        print("验证通过")
        return True

verify_stage()

输出：

验证失败！反例：
  x = 1.0, 2.0
  grad_y = 0.5, -0.3
  grad_x_logical = 0.7  # 正确全局梯度
  gx0 + gx1 = 0.35      # 实际计算值（因未同步，仅为一半）

精准定位：TrainVerify 不仅报告失败，还提供具体反例和违反的等式，直接指向 backward() 中遗漏的 all_reduce。

步骤 7：修复 Bug 并重新验证

修正并行实现，添加缺失的 AllReduce：

# fixed_parallel_linear.py - 修复后的实现
def backward(self, grad_output):
    grad_x_partial = torch.matmul(grad_output, self.weight_shard)
    
    # 修复：添加梯度同步
    dist.all_reduce(grad_x_partial, op=dist.ReduceOp.SUM)  # ← 关键修复
    
    grad_weight = torch.matmul(grad_output.t(), x)
    return grad_x_partial, grad_weight

重新运行 TrainVerify：

验证通过！所有阶段等价性成立。
验证耗时: 0.8 秒（形状缩减后仅需验证 4 个符号变量）

完整工作流总结

步骤	输入	处理	输出	关键技术
1	逻辑模型代码	追踪（tracing）	逻辑 DFG	PyTorch FX
2	并行策略配置	nnScaler 编译	并行 DFG + 血缘	图重写
3	两个 DFG	符号化转换	符号 DFG (sDFG)	Z3 Real 变量
4	sDFG	形状缩减优化	最小形状 sDFG	整数规划求解
5	最小 sDFG	划分为阶段	验证任务队列	后向切片
6	每个阶段	SMT 求解	等价性证明/反例	Z3 求解器
7	所有阶段结果	组合证明	端到端等价性	传递性推理

TrainVerify：基于等价性的分布式大语言模型训练验证方法

介绍

笔记